Circumcircle

A circumcircle is a circle created from three points. The circle circumference (outer edge) must pass on all three points to be considered a circumcircle.

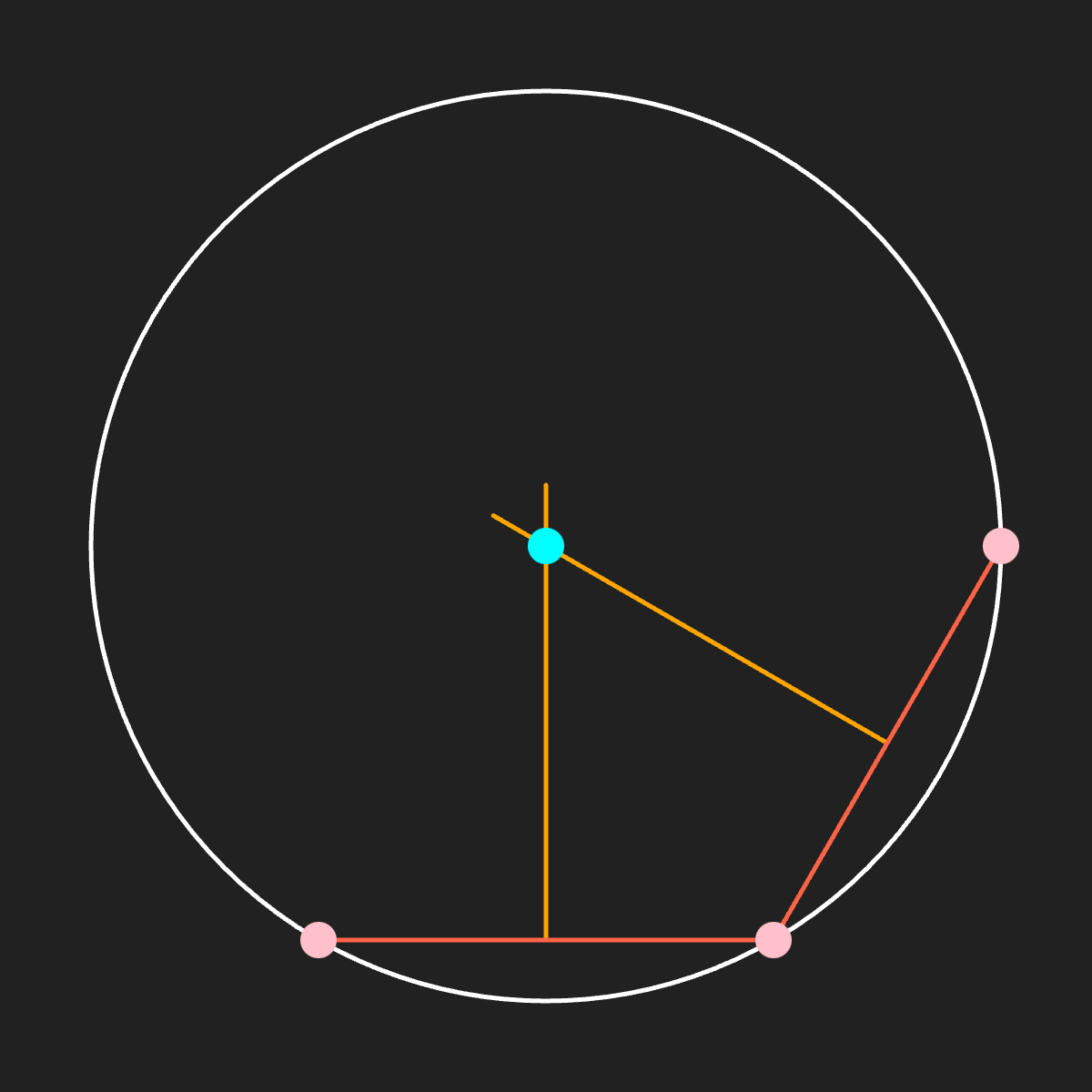
Calculating the circumcircle

There are multiple methods for finding the circumcircle for three given vertices, but this article will only cover one of them.

Find two connecting lines

Given your three vertices (v1, v2, v3), select any two vertex and join them by a line.

line(
  v1.x, v1.y,
  v2.x, v2.y
);

Repeat this for two other different vertices.

line(
  v2.x, v2.y,
  v3.x, v3.y
);

If you were to draw them it would look like the following.

Find the perpendicular lines

Now we need to find both perpendicular lines for the two lines we just created. The perpendicular lines must have one of their vertex placed at the center of the other line.

To find a perpendicular line from a line you can find the first vertex (the mid point of the original line) by calculating the average x and y of the two vertex for that line.

const midX = (v1.x + v2.x) / 2;
const midY = (v1.y + v2.y) / 2;
const midVertex = { x: midX, y: midY };

For the second vertex, we need to rotate the line end segment by 90°. To do so we must rotate from the origin vertex of the line and then move it back to the base position.

1. Create a new vertex at the origin

const v = { x: v2.x - v1.x, y: v2.y - v1.y };

2. Apply the rotation to the vertex

// Calculate the length of the vertex (its magnitude)
const length = Math.sqrt(v.x * v.x + v.y * v.y);
// Calculate the new angle
const angle = Math.atan2(v.y, v.x) + (Math.PI * 2); // Math.PI * 2 == 90°
// Calculate the new position from the angle and the length (polar coordinate)
v.x = Math.cos(angle) * length;
v.y = Math.sin(angle) * length;
// Add the midVertex vertex as its origin
v.x += midVertex.x;
v.y += midVertex.y;

We do the above for both the lines that we defined earlier. We will call the four new vertices as (v4, v5, v6, v7).

Let's draw the new lines and see where they end up.

line(
  v4.x, v4.y,
  v5.x, v5.y
);
line(
  v6.x, v6.y,
  v7.x, v7.y
);

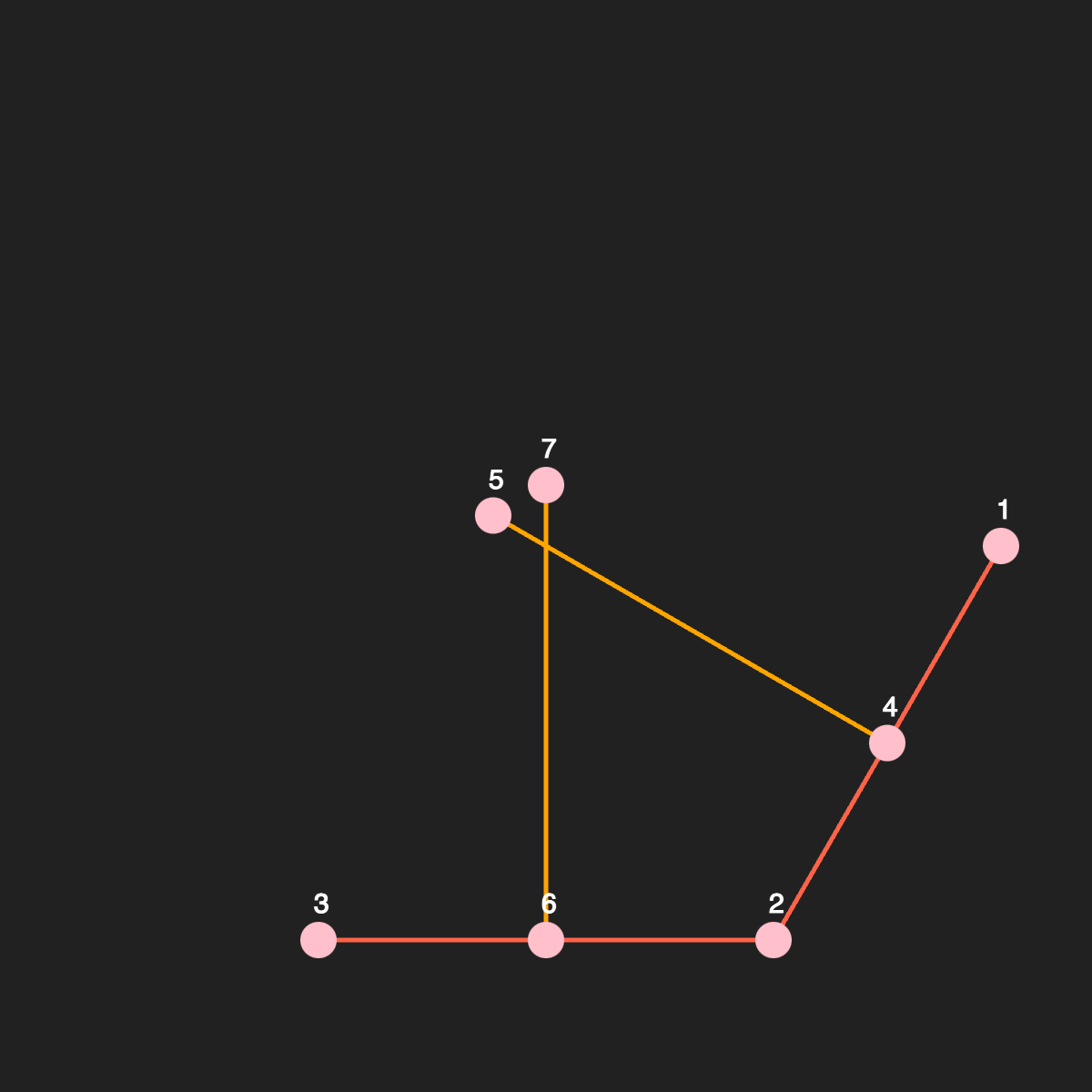
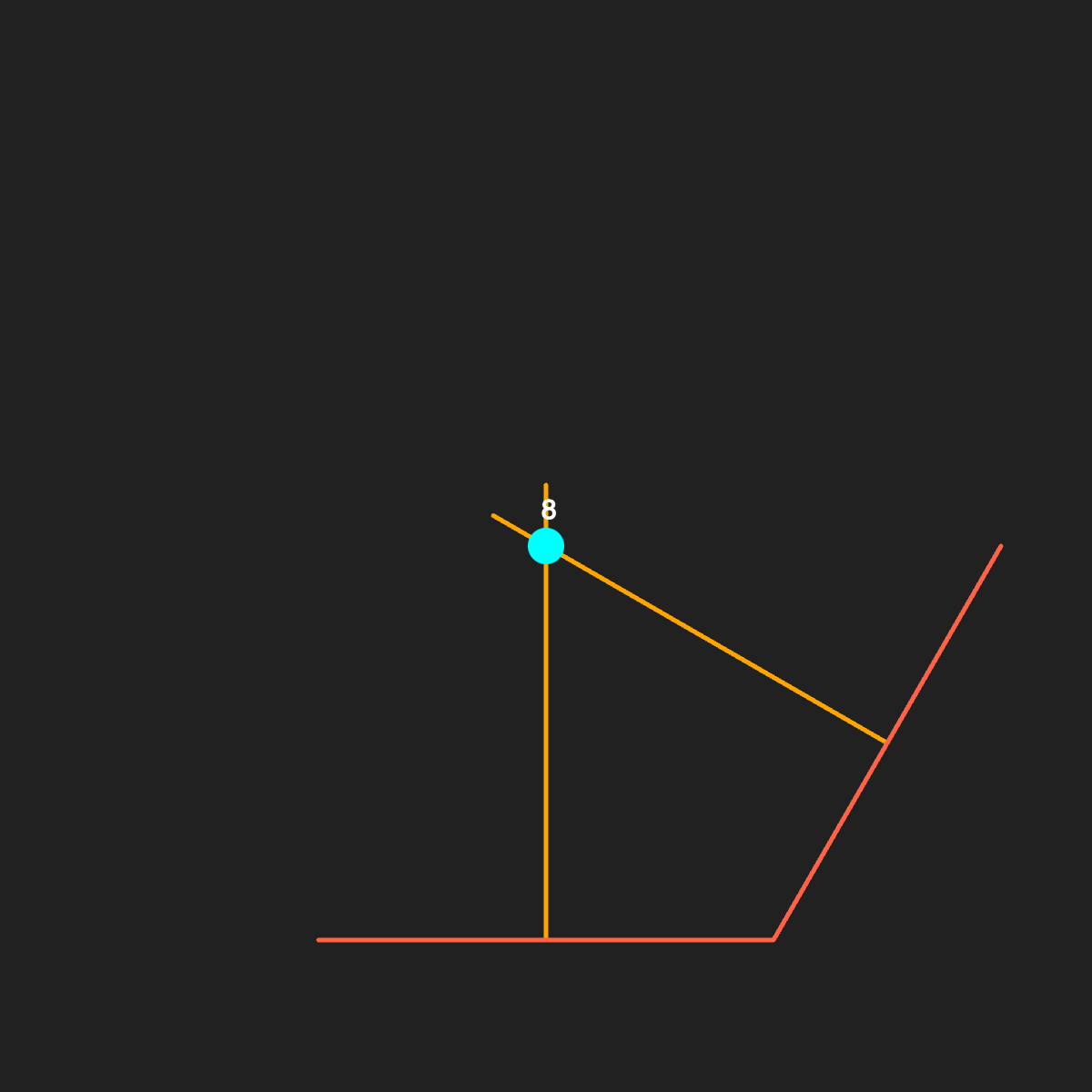
Find the intersection vertex

We must find the intersection vertex between the two perpendicular line which will be the center of our circle.

The next formula is taken from Wikipedia, the formula is used to find the intersection vertex of two (non-parallel lines).

const x1 = v4.x;
const y1 = v4.y;
const x2 = v5.x;
const y2 = v5.y;
const x3 = v6.x;
const y3 = v6.y;
const x4 = v7.x;
const y4 = v7.y;

Here I'm creating temp variables to have an easier time reading the formula.

const denominator = (x1 - x2) * (y3 - y4) - (y1 - y2) * (x3 - x4);
if (denominator === 0) {
  // Handle the case where the lines are parallel (no intersection)
}

const x = ((x1 * y2 - y1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * y4 - y3 * x4)) / denominator;
const y = ((x1 * y2 - y1 * x2) * (y3 - y4) - (y1 - y2) * (x3 * y4 - y3 * x4)) / denominator;
const v8 = { x, y };

We can also draw the new vertex we found (v8).

Find the radius of the circle

The last step is to find the radius of our circle. To do so is pretty easy, all we need to do is to find the distance between any of the three original vertices and the center vertex.

const radius = Math.sqrt(
  Math.pow((v1.x - v8.x), 2) +
  Math.pow((v1.y - v8.y), 2)
);

Drawing the circle using the center and the radius

ellipse(v8.x, v8.y, radius, radius);

As we can see in the image above all of our original vertices are passing through the circle circumference. Which we can now call the circumcircle of our vertices.

More information

For more information and ways to compute the circumcircle I would direct you to the wikipedia page.